При поддержке гранта РФФИ № 12-02-31068 (МОЛ_а, мой первый грант) выполняются работы по исследованию поля притяжения несферических тел Солнечной системы.
Определение параметров гравитационных полей планет – одна из важнейших задач космических исследований. Анализ особенностей движений естественных спутников и КА, обращающихся на околопланетных орбитах, служит источником информации о параметрах внешних гравитационных полей и о внутренних структурах планетных тел. Эволюции орбитального движения КА в основном задаются особенностями центрального гравитационного поля исследуемого небесного тела.
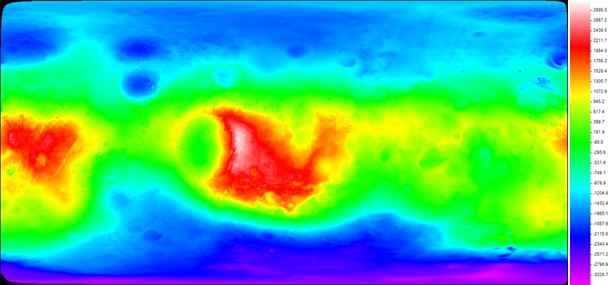
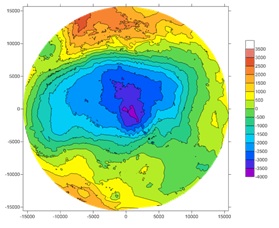
Проект направлен на разработку методики представления и расчета потенциала притяжения существенно несферических тел солнечной системы непосредственного на его поверхности, на примере Фобоса.
Ожидаемые научные результаты, которые планируется получить по завершению проекта:
Этапы исследования:
1. Сбор и детальный анализ имеющейся информации о существующих пространственных цифровых моделях рельефа (ЦМР) поверхности Фобоса (как наиболее информационно богатого несферического небесного тела).
2. Подготовка моделей к исследованию.
2.1 Пересчет нерегулярной структуры ЦМР на регулярную сетку (матрица высот).
2.2 Оценочный анализ точности перехода к регулярной матрице высот.
3. Разработка алгоритма вычисления потенциала на поверхности Фобоса без использования аппроксимирующих полиномов.
3.1 Создание рабочей модели для описанной в статье Огородова Л.В., Надеждина И.Е. «Внешний потенциал притяжения однородной модели Фобоса» методики, обеспечивающей вычисление потенциала притяжения усеченной пирамиды, со сферическими основаниями.
3.2 Вычисление потенциала притяжения предложенным методом для сферы и эллипсоида вращения.
3.3 Критический анализ полученных результатов.
4. Алгоритмитизация метода вычисления потенциала притяжения с использованием матрицы высот.
5. Вычисление потенциала поля притяжения Фобоса по данным КА «Mars Express» по состоянию на 2011 год.
6. Сравнение вычисленного потенциала притяжения с потенциалом, полученным разложением по сферическим функциям для различных расстояний от поверхности Фобоса.
За время исследования выполнены первые 2 этапа работы. Проанализированы существующие ЦМР Фобоса — данные, послужившие основой для ЦМР, и методы создания. В МИИГАиК была создана ЦМР на основе данных КА Mars Express и Viking Orbiter-1,2. Проанализированные ЦМР Фобоса, включая полученную в МИИГаиК, сведены в одну таблицу (Таблица 1).
Полученная ЦМР подготовлена для дальнейших исследований – выполнен пересчет нерегулярной структуры ЦМР на регулярную сетку. Регулярная модель рельефа была получена на базе векторных данных с шагом 0.3 градуса по широте и долготе с физическими размерами 601×1201 ячеек. Размер каждой ячейки приблизительно соответствует 50 м. Из модели были исключены грубые ошибки, так что окончательная точность модели может быть оценена с СКО = 32 м. Окончательно сформированная модель отнесена к геометрическому центру Фобоса, точность которого определяется с СКО = 44 м.
В настоящее время исследования продолжаются. Модели рельефа Фобоса:
| Год | Автор | Метод создания и краткое описание модели |
| 1974 | T.C. Duxbury | Координаты 38 опорных точек, измеренных на изображениях Mariner 9 |
| 1978 | R. J. Turner | — опорная сеть из 260 точек по изображениям КА — Гипсовые модели на основе сети |
| 1989 | P.C. Thomas | Эллипсоидальная модель, полученная по лимбовым определениям Mariner 9 |
| 1989 1992 |
R. M. Batson et al. | ЦМР путем интерполяции между опорными точками. Далее полученную ЦМР была использована для ортотрансформирования изображений и создания мозаики Фобоса |
| 1993 | P.C. Thomas | Численная модель, полученная по изображениям VO с контролем по лимбовым определениям, используя изображения Mariner 9 |
| 1993 | D.P. Simonelli et al. | Численная модель с разрешением 2х2?, полученная с использованием лимбовых определений и опорных точек. Для построения использовались 60 изображений VO с разрешением 6-170 м/пиксель |
| 1991 | T.C. Duxbury | Для координат опорных точек были подобраны коэффициенты сферических гармоник до 8 степени и порядка. Около 315 кратеров (с отношением глубины к диаметру 0.1-0.2) были добавлены отдельно для детализации модели. Используя данные функции была создана численная модель с шагом 0.5? (порядка 100 м/пиксель). Точность данной модели варьируется от 100 до 500 м |
| 1994 | Г.А. Аванесов | Численная модель. Изначально была построена по данным Тернера (Turner 1978) и содержала 50833 точки. В дальнейшем была уточнена в ходе визуального сравнения со снимками «Викинг-1,-2» |
| 2010 2012 |
K.Willner | 60 изображений HRSC MEX различных каналов (ср высота орбит 110 км) и 16 изображений VO (ср высота орбит 929 км), с разрешением лучше 80 м/пиксель. Измерение пикетов производилось в автоматическом режиме. Разрешение ЦМР 100 м/пиксель, высотная точность – 10-80 м |
| 2012 | МИИГАиК | 117 изображений MEX и VO. Пикеты измерялись вручную в стерео режиме в характерных участках рельефа, поэтому ЦМР имеет нерегулярную структуру. Среднее расстояние между точками составляет 0.6?. ЦМР отражает как глобальный, так и локальный рельеф, за счет содержания определенных вручную структурных линий (кратеры и борозды). |
Список литературы:
1. Аванесов Г.А., Жуков Б.С., Зиман Я.Л. и др. Телевизионные исследования Фобоса // М.: Наука, 1994.-168 с. –ISBN 5-02-000298-4.
2. Зубарев А.Э., Надеждина И.Е., Конопихин А.А. Проблемы обработки данных дистанционного зондирования для моделирования фигур малых тел Солнечной системы // Современные проблемы дистанционного зондирования Земли из космоса. 2012. Т. 9. № 4. С. 277-285.
3. Batson R. M., Edwards K., and Duxbury T. C. Geodesy and cartography of the Martian satellites // Mars, 1992. P. 1249-1256.
4. Duxbury T.C. PHOBOS – Control network analysis // Icarus. 1974. V. 23. P. 290-299.
5. Duxbury T. C. The figure of PHOBOS // Icarus. 1989. V. 78. P. 169-180.
6. Duxbury T. C. An analytic model for the PHOBOS surface // Earth Planet Sci. Lett. 1991. V. 39. P. 355–376.
7. Simonelli D.P., Thomas, P.C., Carcich, B.T., Veverka, J. The generation and use of numerical shape models for irregular solar system objects // Icarus. 1993. V. 103. P. 49–61.
8. Thomas P.C. The shapes of small satellites // Icarus. 1989. V. 33. P. 116-140.
9. Turner R. J. A model of PHOBOS // Icarus. January 1978. V. 33. P. 116-140. doi: 10.1016/0019-1035(78)90028-3 .
10. Willner K., Oberst J., Hussmann H. et al. Phobos Control Point Network, Rotation, and Shape // Earth Planet. Sci. Lett. 2010. V. 294. P. 541–546.